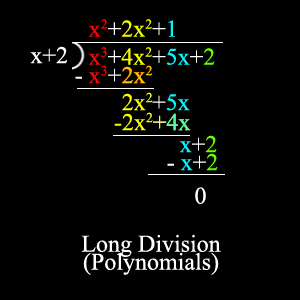posted by Jeff R. at 7:46 p.m.

First thing's first, we started the class by having Ms. Armstrong to post the answer key for the S1 Review at the back of the room. So if you need to correct your work, check it out sometime. Anyway, we were in groups once again. Ms. Armstrong turned on the projector and then we started taking down notes on "Multiplying Polynomials".
*Here are the notes incase you were lazy in class and didn't copy them :P
Multiplying Polynomials
 = 12
= 12
Multiplying means "finding the area of a rectangle".
Example:
 Find the area.
Find the area.
Now, there are 3 ways that you can do to find the area or to multiply the polynomials. It depends on which one you are most comfortable with:
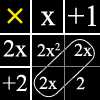 The first way of multiplying polynomials is to use the "Tic Tac Toe" format. Using the above question, it will look like the image on the left. The yellow "x" is the multiplication sign. The "x+1" represents the width, and the "2x+2" represents the length of the rectangle. So it'll be like, (2x)(x) = 2x2 and so forth. Then you add the like terms which are the ones that are circled.
The first way of multiplying polynomials is to use the "Tic Tac Toe" format. Using the above question, it will look like the image on the left. The yellow "x" is the multiplication sign. The "x+1" represents the width, and the "2x+2" represents the length of the rectangle. So it'll be like, (2x)(x) = 2x2 and so forth. Then you add the like terms which are the ones that are circled.
 The second way is using the "Algetiles". This format is like the Tic Tac Toe format except it is presented in images. If you don't know what the images represents, see the previous post.
The second way is using the "Algetiles". This format is like the Tic Tac Toe format except it is presented in images. If you don't know what the images represents, see the previous post.
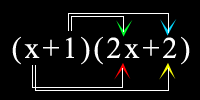 The last one is everybody's favourite, the "Distributive Property". You first do the red one then the yellow then the green then the blue. So the answer would be:
The last one is everybody's favourite, the "Distributive Property". You first do the red one then the yellow then the green then the blue. So the answer would be:
= 2x2 + 2x + 2x + 2
= 2x2 + 4x + 2 (the like terms were added to simplify)
Dividing Polynomials
Dividing polynomials isn't that hard once you got how to do it properly. On an equation like this:
16x4y5 - 8x8y9
------------------------------
4xy4
Reminder that the denominator applies to all the polynomials on top. So here's how you divide polynomials:
i. Divide the coefficient (the number before the variable) on the denominator from the coefficient on the numerator. (Eg: 16 divided by 4)
ii. Subtract the exponents
iii. Then do the same thing with the second monomial.
**The final answer will look like this: 4x
3y - 2x
7y
5Like the multiplication of polynomials, dividing polynomials also have different ways to represent the equation:
i. (4x
2+x
3+5+2) division sign (x+2)
ii. (4x
2+x
3+5+2) / (x+2)
iii. Divide (4x
2+x
3+5+2) by (x+2)
iv. Find the length of a rectangle if the AREA is (4x
2+x
3+5+2) and the width is (x+2).
Long Division:
Before you solve an equation in long division, you must make sure that your terms are in descending order. If it's 4x
2+x
3+5+2, it should be x
3+4x
2+5+2, since the exponent "3" is higher than the exponent "2" even though it has a coefficient before it and the other one doesnt.
Long Division in polynomials is the same thing as dividing long division normally.
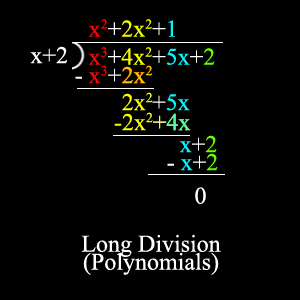
Between the notes, we've had an activity. The activity was to find the area of this:

Our Solution
My group started to find the area of the "whole rectangle" (on the left side, picture 2). Then subtracted the area of the small rectangle (in gray).
Our equation turned out to be like this:
The area of the "whole rectangle".
A = (4x - 1)(3x + 5)
A = 12x2 20x - 3x - 5
The area of the smaller rectangle (in gray).
A = (2x - 3)(3x - 1)
A = 6x2 - 2x - 9x + 3
A = 6x2 - 11x + 3
Subtract them together.
A = (12x2 + 17x - 5) - (6x2 - 11x + 3)
Note: To subtract polynomials, change the "-" sign (in the middle) to "+" then change the rest of the right side to it's opposite signs.
A = 12x2 + 17x - 5 + (-6x2) + 11x - 3
A = 6x2 + 28x - 8
Aaaand that's it. Pheew, did I do this blogging right?
Homework: Exercise #1 - If you're not done yet.
Homework: Exercise #3
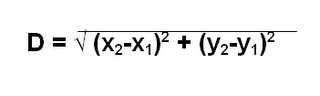 Recall: A point on a graph is denoted by the coordinates (x,y)
Recall: A point on a graph is denoted by the coordinates (x,y)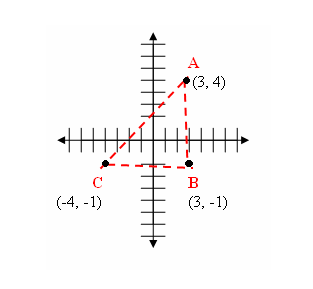
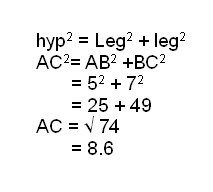 But if you used the distance formula, you wouldn't need the 'spaces' because using this formula would give you the sides of all the area all in one equation.
But if you used the distance formula, you wouldn't need the 'spaces' because using this formula would give you the sides of all the area all in one equation.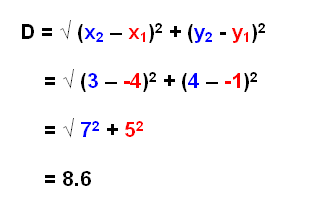 It doesn't matter if you switched the 1 as (3, 4) and 2 as (-4, -1).
It doesn't matter if you switched the 1 as (3, 4) and 2 as (-4, -1).
 = 12
= 12 Find the area.
Find the area.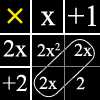 The first way of multiplying polynomials is to use the "Tic Tac Toe" format. Using the above question, it will look like the image on the left. The yellow "x" is the multiplication sign. The "x+1" represents the width, and the "2x+2" represents the length of the rectangle. So it'll be like, (2x)(x) = 2x2 and so forth. Then you add the like terms which are the ones that are circled.
The first way of multiplying polynomials is to use the "Tic Tac Toe" format. Using the above question, it will look like the image on the left. The yellow "x" is the multiplication sign. The "x+1" represents the width, and the "2x+2" represents the length of the rectangle. So it'll be like, (2x)(x) = 2x2 and so forth. Then you add the like terms which are the ones that are circled. The second way is using the "Algetiles". This format is like the Tic Tac Toe format except it is presented in images. If you don't know what the images represents, see the previous post.
The second way is using the "Algetiles". This format is like the Tic Tac Toe format except it is presented in images. If you don't know what the images represents, see the previous post.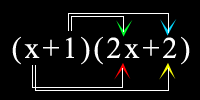 The last one is everybody's favourite, the "Distributive Property". You first do the red one then the yellow then the green then the blue. So the answer would be:
The last one is everybody's favourite, the "Distributive Property". You first do the red one then the yellow then the green then the blue. So the answer would be: