Hey Gummy Bears,
This is The Scribe List - Round 2. Every possible scribe in our class is listed here. This list will be updated every day. If you see someone's name on this list in Blue Font then you CANNOT choose them as the scribe for the next class.This post can be quickly accesed from the [Links] list on the right hand sidebar. Check the list before you choose a scribe for tomorrow's class when it is your turn to do so. At the end of your scribe post, let us know who will be scribing tomorrow.
Dinh--------------- Edward
Michele H. ----- Thamie---------
Xuan ---------- Christine ----------- Don
Donavon ------ Jeff -------------- Meagan
Jamie -------------- Kim T.
Destini -------- Alanna -------------- Emman
Kevin --------- Chris --------------- Cory
Shelly-------- Haiyan
Paulo ---------- Daureen ----------- Jhonaleen
Welcome to a world where creativity, ingenuity, and mathematics mesh together to create Grade 10 Precalculus math.
posted by Ms. Armstrong at 9:00 a.m.
Hi Gummy Bears,
As you may have noticed the html code for 'square root' is not working. I have done some research on the internet and everything seems to indicate that I coded correctly. I have tried the code <&radic>, but it doesn't work either. Does anyone have any programming experience that could help us format a radical? 2 Bonus marks on the next test for the person that solves our trouble.
Ms. Armstrong
As you may have noticed the html code for 'square root' is not working. I have done some research on the internet and everything seems to indicate that I coded correctly. I have tried the code <&radic>, but it doesn't work either. Does anyone have any programming experience that could help us format a radical? 2 Bonus marks on the next test for the person that solves our trouble.
Ms. Armstrong
Friday, October 27, 2006
posted by S. Tao at 3:56 p.m.
Today in class Mrs. Armstrong showed us how to use the html codes for this blog:
Egs:
1)38 = what number times it self 3 times will give 8
38 = 81/3
38 = 2
6)3 43 = 31/231/4
= 32/4+1/4 = 33/4 = 433
How to do it on the calulator:
Option 1 8yx 0.3333333 = 1.9999999.... (not accurate)
Option 2 8yx 1 ab/c = 2 (only if you have the ab/c button on your calulator)
Homework: finishing the puzzle Mrs. Armstrong gave us
Important!!!! On Monday we have a Quiz!!
- Exponents: x< .sup>1/2 (no spaces and periods)
- Square root: < .sqrt >x+2< /sqrt > (no spaces and periods)
Egs:
1)
3
3
6)
= 32/4+1/4 = 33/4 = 4
How to do it on the calulator:
Option 1 8yx 0.3333333 = 1.9999999.... (not accurate)
Option 2 8yx 1 ab/c = 2 (only if you have the ab/c button on your calulator)
COMMON PERFECT SQUARES AND CUBES TABLE
Heres an link that will show you the laws of rational exponents
Homework: finishing the puzzle Mrs. Armstrong gave us
Important!!!! On Monday we have a Quiz!!
The person who is going to blog next is...... Eden!
Friday, October 20, 2006
posted by Chris at 11:56 p.m.
First of all, currently, Jamie's blog entry is not up on the main page (since it's saved as a draft at the moment) but you can view it by clicking on this text and looking under the post title of 'Putting It All Together.'
Today in class, we had our Analytic Geometery Unit Test, which I'm sure we were all happy to do ;D. The test lasted for the whole period, and it was basically a small review on the unit. That's all we had a chance to do today, which means no notes or exercies.
Important Reminder
As Jamie mentioned in her post, our completed units are to be handed in on Monday, October 23rd, 2006
With the following included:
All of this presented in an organized duotang with your name on the cover.
This sums up my post and all we did in Friday's class (October 20th, 2006), have a good weekend everybody and we'll see you on Monday.
Also, Monday's blogger will be: Kim D.
Today in class, we had our Analytic Geometery Unit Test, which I'm sure we were all happy to do ;D. The test lasted for the whole period, and it was basically a small review on the unit. That's all we had a chance to do today, which means no notes or exercies.
Important Reminder
With the following included:
- A title page which is based on the unit. (Which means don't put something that has nothing to do with Analytic Geometry on it, Ex. Superman.)
- A completed table of contents. (I'm pretty sure all exercises were posted up in previous blog entries so check them to see if you missed anything)
- All of this unit's completed work/assignments and notes.
- *Self-Reflection Tags which are required to be completed and included otherwise it will not be taken in.*
All of this presented in an organized duotang with your name on the cover.
This sums up my post and all we did in Friday's class (October 20th, 2006), have a good weekend everybody and we'll see you on Monday.
Also, Monday's blogger will be: Kim D.
Monday, October 16, 2006
posted by --thamie-- at 6:36 p.m.
a message to my group (meagan, kriszelle, daureen, xuan)...
i finished the distances and stuff w/ the slide and made a title page just in case...i didnt do the write up but im sure meagan's doing it...right?
i finished the distances and stuff w/ the slide and made a title page just in case...i didnt do the write up but im sure meagan's doing it...right?
Wednesday, October 11, 2006
posted by man at 6:13 p.m.
Todays math class we talk about the 3 methods in graphing. Im here to explain again this methods so that we can all understand it.
Graphing Method #1 (Table of Values)
- "table of values" shows the relationship between x and y given by any equation.
We can pick any value for x and use the equation to solve y.
y=x+1 (y is equal to the value of x plus one)
let x = 1
y=x+1 Each one of this pairs values represents
y=1+1 a points on our line. These are then easily
y=2 graph.
let x = 2
y=x+1
y=2+1
y=3
let x = 3
y=x+1
y=3+1
y=4
Graphing Method # 2 (Intercept)
- When you speak of intercepts, it helps to know which one you're referring to.
In the plane, unless a line is parallel to either the x-axis or the y-axis, it will intersect
both axis sometime. We know this because two non-parallel lines in the same plane
will intersect sometime.
x-intercept
The x-intercept is where the graph crosses the x axis.
The word 'intercept' looks like the word 'intersect'.
Think of it as where the graph intersects the x-axis.
With that in mind, what value is y always going to be on the x-intercept? No matter
where you are on the x-axis, y’s value is 0, that is a constant.
eg.
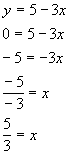
y-intercept
If the x-intercept is where the graph crosses the x-axis where do you think the graph crosses for the y-intercept? If you said the y-axis, you are absolutely right.
This time it is x’s value that is 0. Any where you would cross the y-axis, x’s value is always 0.
eg.
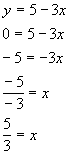
Graphing Method #3 (Slope-Intercept)
- The slope of a line measures the steepness of the line.
- Most of you are probably familiar with associating slope with "rise over run".
Rise means how many units you move up or down from point to point.
On the graph that would be a change in the y values.
Run means how far left or right you move from point to point. On the graph,
that would mean a change of x values.
*equation: slope = y=mx+b
eg.
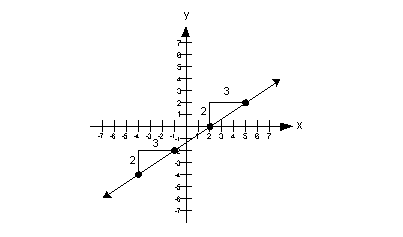
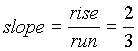
Every straight line can be represented by an equation: y = mx + b.
The coordinates of every point on the line will solve the equation if you substitute
them in the equation for x and y.
The slope m of this line - its steepness, or slant - can be calculated like this:
m = change in y-value
change in x-value
*if theirs question ask me..
next one to blog is jessica
Tuesday, October 10, 2006
posted by Ms. Armstrong at 12:45 p.m.
Hey Gummy Bears,
Here are some online multiple choice questions to help you determine which topics you may need to focus on while you're studying. You can try a quiz more than once because most of the quizzes have a data base of several extra questions.
Slope
Writing Equations
Writing Equations in slope intercept form
Graphing Equations
Parallel and Perpendicular lines
Midpoint of a Line Segment
Hope this helps.
Ms. Armstrong
Here are some online multiple choice questions to help you determine which topics you may need to focus on while you're studying. You can try a quiz more than once because most of the quizzes have a data base of several extra questions.
Slope
Writing Equations
Writing Equations in slope intercept form
Graphing Equations
Parallel and Perpendicular lines
Midpoint of a Line Segment
Hope this helps.
Ms. Armstrong
Tuesday, October 03, 2006
posted by siopao at 8:31 p.m.
These or the notes from today's class(October 2/2006) just in case you weren't taking notes or weren't in class today at all:
*first of three ways to graph a line
Equations of straight lines can be written in three ways:
-1) Ax+By+C= 0
-2) Ax+By=C
*3) y=mx+b m=slope b=intercept
1) and 2) are standard form
3) is slope intercept form
-in order to graph from a T.O.V. (table of values), the equation must be in "slope intercept form"
while graphing the T.O.V. you should think:
a) is it in slope intercept form?
and make a:
b) two variable table
eg) graph y=2x+3 using a table of values
a) yes
b)

*you only need 3 pts. to graph a line*
eg) let x have a value of -1,0,1
graph 4x+2y=12 using T.O.V.

eg) graph y=-4+0x

eg)

Well that's all for notes, I hope they helped the people looking for notes
So we were assigned all of exercise 5 in our red duotang and we were also responsible for "marking" one of our class mates completed unit.
-base the marks on the title page (needs to contain diagrams appropriate to the unit in this case polynomials, color and creativity) out of 5
-table of contents (a complete list of notes and assignments covered in class, and if included in completed unit must have a checkmark) out of 5
*first of three ways to graph a line
Equations of straight lines can be written in three ways:
-1) Ax+By+C= 0
-2) Ax+By=C
*3) y=mx+b m=slope b=intercept
1) and 2) are standard form
3) is slope intercept form
-in order to graph from a T.O.V. (table of values), the equation must be in "slope intercept form"
while graphing the T.O.V. you should think:
a) is it in slope intercept form?
and make a:
b) two variable table
eg) graph y=2x+3 using a table of values
a) yes
b)

*you only need 3 pts. to graph a line*
eg) let x have a value of -1,0,1
graph 4x+2y=12 using T.O.V.

eg) graph y=-4+0x

eg)

Well that's all for notes, I hope they helped the people looking for notes
So we were assigned all of exercise 5 in our red duotang and we were also responsible for "marking" one of our class mates completed unit.
-base the marks on the title page (needs to contain diagrams appropriate to the unit in this case polynomials, color and creativity) out of 5
-table of contents (a complete list of notes and assignments covered in class, and if included in completed unit must have a checkmark) out of 5
-Completeness (all class work and noted included, assignments completed, organized in same order as stated on the table of contents)out of 25
-Neatness(all items are neat, legible, and organized)out of 5
-And last but certainly not least the most important of all, the self reflections(I'm proud, I've improved, I still need to work on and trash it tags are included, reflections show insight into self improvement and learning)out of 10
if you need more explanation on the completed unit go to "unit one" by Xuan
oh yeah, before I forget the next person to post will be Kimberley
Monday, October 02, 2006
posted by meagan at 7:09 p.m.
 The midpoint of a line segment is the point directly in the center of the line. Here is the midpoint formula.
The midpoint of a line segment is the point directly in the center of the line. Here is the midpoint formula.
This is like finding the average of the x's and y's

Here are some examples:
1.) Find the center of a circle whos end points of the diameter are D(3,-2) and E (-2,4)
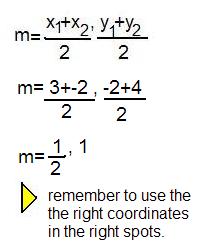
2.) (9,11) is the midpoint and the end points are at (x,12) and (B, y) find xy

It doesnt matter what variable is used. so dont get confused by that. Just remember to always plug in the information that you have.
Thats about all we learned on fridays class. exept that ms.Armstrong worked for her dad's candy company and her children slept in shopping carts. hehe.
Dont forget that the homework was exersise 5 and expect a quiz on midpoints and distance on wednesday. not on graphing.
