posted by Jeff R. at 9:25 p.m.
Today's class was pretty easy and hard at the same time. Easy because we only had one lesson to think about. Hard because the lesson that we learned was a little too difficult for me (I don't know about you guys). But I'll try my best to make this post as understandable as possible. Okay, here it goes.
Ms. Armstrong gave us a yellow sheet of paper with 2 questions on it. The first question didn't make sense at all so even Ms. Armstrong had some confusion. So we'll omit that so we can focus on the more important stuff.
The second question was to determine the angles that would produce the following ratios:
a) sin(x) = .707 acute angle = ___ obtuse angle = ___
b) cos(x) = .940 acute angle = ___ obtuse angle = ___
c) tan(x) = 11.43 acute angle = ___ obtuse angle = ___
d) cos(x) = -.970 acute angle = ___ obtuse angle = ___
e) sin(x) = -.5 acute angle = ___ obtuse angle = ___
f) tan(x) = -1.43 acute angle = ___ obtuse angle = ___
Note: It's not as easy at it looks. Here's how you solve each of the above questions but first, keep in mind to round all of your degrees to a whole number.
1) To find the acute angle, punch in the equation in your calculator:
2nd function > SIN/COS/TAN button = SIN/COS/TAN-1 (given ratio).
Let's use letter a) for an example.
So, 2nd funct. > SIN button = SIN-1 (.707) : the answer is 45o.
The degree that comes out of this equation is your acute angle.
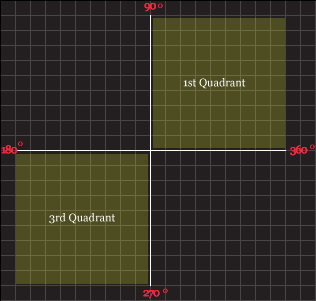
2) Now let's find the obtuse angle. To find the obtuse angle, you will need to know which quadrant does the given ratio belongs to.
The
positive sine ratio belongs to the the first & second quadrants.

The positive cosine ratio belongs to the first and fourth quadrants
And the positive tangent ratio belongs to the first and third quadrant.
Since the positive sine ratio lands on the 2nd quadrant, you have to subtract your acute angle from 180 degrees since the acute angle is the measurement of how far is your hypoteneuse from the 2nd quadrant's degree (which is 180 degrees).
When finding the positive cosine ratio, subtract the acute angle from 360 degrees since it lands on the 4th quadrant.
Lastly, if you're finding the positive tangent ratio, subtract the acute angle from 270 degrees or add the acute angle to 180 degrees.
And now you're done your positive ratios! Here's how I solved the first three questions:
a) sin(x) = .707 which is 45o.
Now, follow the rules above: 180 - 45 = 135o
acute angle = 45o
obtuse angle = 135o
b) cos(x) = .940 which is 20o
360 - 20 = 340o
acute angle = 20o
obtuse angle = 34o
c) tan(x) = 11.43 which is 85o
acute angle = 85o
obtuse angle = 265o
_______________________
Now the negatives (questions 4 - 6). The negative ratios are a little bit different.
1) To find the acute angle of a negative ratio, do the same thing as how you would find the acute angle of a positive ratio, here's a refresher:
punch in the equation in your calculator:
2nd function > SIN/COS/TAN button = SIN/COS/TAN -1 (given ratio).
Let's use letter d) for an example.
So, 2nd funct. > SIN button = COS-1 (-.970)
When I used my scientific calculator, what I got was -166 degrees. But that's the not the final answer. Remember, the acute angle should be positive. So the answer will be 166 degrees (yes, just randomly take out the negative sign because I don't think that there is a mathematical format for how to change a negative degree to a positive degree).
2) Then let's find the obtuse angle. Do the same thing as you did to the positive ratios.
d) cos(x) = -.970 which is 166 degrees
acute angle = 166 degrees
obtuse angle = 194 degrees
e) sin(x) = -.5 which is 30 degrees
acute angle = 30 degrees
obtuse angle = 330 degrees
f) tan(x) = -1.43 which is 55 degrees
acute angle = 55 degrees
obtuse angle = 235 degrees
And that's it! Sorry for the delay guys, there was too much in my head, although it's done now (: we also got our unit tests back then we went over some of the questions. Congratulations to the all stars! And oh yeah, I pick Desitini to blog next since the people I know didn't want to since they're "busy", haha. Oh yeah, and reminder to redo question #2 on exercise 18 using the above steps.
Ms. Armstrong, a video for this one is kind of hard to find. If anyone can help me , that'll be great :)