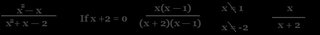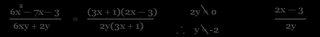Adding / Subtracting
a few practice Questions
We started the notes we an example - Probably to see what we knew about the topic.
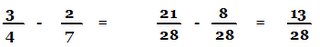
To simplify algebraic Fractions:
1)Factor/ Find the LCD (lower common denominator)
*multiply the denominators together to find a common denominator
2)Change both fractions to have the same denominator
3)Find the restrictions
4)Add/subtract
5)Simplify
6)Re-check Restrictions
eg)
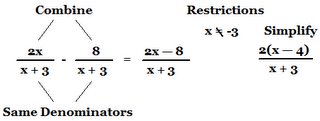
eg)
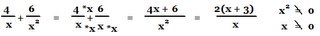
a few practice Questions
We started the notes we an example - Probably to see what we knew about the topic.
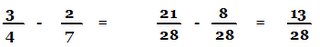
To simplify algebraic Fractions:
1)Factor/ Find the LCD (lower common denominator)
*multiply the denominators together to find a common denominator
2)Change both fractions to have the same denominator
3)Find the restrictions
4)Add/subtract
5)Simplify
6)Re-check Restrictions
eg)
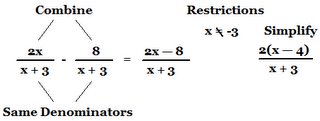
eg)
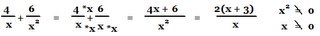
Ex 44 is homework
omit 20