To late for posting.lol!Well this is last mondays lesson.Relation(Domain and Range)
"Relation"
A relation is any subset of a Cartesian product. For instance, a subset of , called a "binary relation from to ," is a collection of ordered pairs with first components from and second components from , and, in particular, a subset of is called a "relation on ." For a binary relation , one often writes to mean that is in .
Eg.
(2,0),(1,5),(3,8),(4,1) ...(any set of ordered pairs are "relation")
The concept of a relation is a generalization of 2-place relations, such as the relation of equality, denoted by the sign "=" in a statement like "5 + 7 = 12," or the relation of order, denoted by the sign "<" in a statement like "5 < 12". the concept of a relation is a generalization of 2-place relations, such as the relation of equality, denoted by the sign "=" in a statement like "5 + 7 = 12," or the relation of order, denoted by the sign "<" in a statement like "5 < 12".
Relations are classified according to the number of sets in the cartesian product, in other words the number of terms in the expression:
Unary relation or property: L(u)
Binary relation: L(u, v) or u L v
Ternary relation: L(u, v, w)
Quaternary relation: L(u, v, w, x)
Domain and Range
Domain:
For a function f defined by an expression with variable x, the implied domain of f is the set of all real numbers variable x can take such that the expression defining the function is real. The domain can also be given explicitly.
Range:
The range of f is the set of all values that the function takes when x takes values in the domain.
The y-values.
This list of points, being a relationship between certain x's and certain y's, is a relation. The domain is all the x-values, and the range is all the y-values. You list the values without duplication:
{(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} This are the set of numbers.
domain: {2, 3, 4, 6}
range: {–3, –1, 3, 6}
You can see how we put the numbers in domain and range. All the x were put to domain and all y were put in range..
Well i hope this things will help you:)Good luck
Welcome to a world where creativity, ingenuity, and mathematics mesh together to create Grade 10 Precalculus math.
Thursday, January 11, 2007
posted by Ms. Armstrong at 12:08 p.m.
Hey Gummy Bears,
I thought you might enjoy this Jeopardy Game that quizzes you on relations, functions, and direct variation. Make sure you use function notation when typing in your answer or it will mark you incorrect. For example...If it asks what is the function, you can't type in 2x+3 . You must type f(x)=2x+3.
I thought you might enjoy this Jeopardy Game that quizzes you on relations, functions, and direct variation. Make sure you use function notation when typing in your answer or it will mark you incorrect. For example...If it asks what is the function, you can't type in 2x+3 . You must type f(x)=2x+3.
Tuesday, December 12, 2006
posted by siopao at 9:04 p.m.
Adding / Subtracting
a few practice Questions
We started the notes we an example - Probably to see what we knew about the topic.
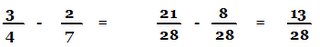
To simplify algebraic Fractions:
1)Factor/ Find the LCD (lower common denominator)
*multiply the denominators together to find a common denominator
2)Change both fractions to have the same denominator
3)Find the restrictions
4)Add/subtract
5)Simplify
6)Re-check Restrictions
eg)
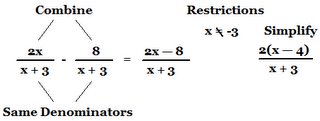
eg)
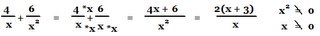
a few practice Questions
We started the notes we an example - Probably to see what we knew about the topic.
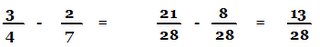
To simplify algebraic Fractions:
1)Factor/ Find the LCD (lower common denominator)
*multiply the denominators together to find a common denominator
2)Change both fractions to have the same denominator
3)Find the restrictions
4)Add/subtract
5)Simplify
6)Re-check Restrictions
eg)
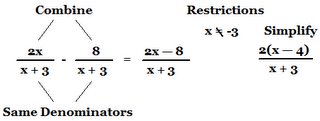
eg)
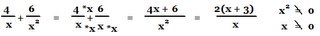
Ex 44 is homework
omit 20
posted by siopao at 5:59 p.m.
The connection between numbers (fractions) and reducing expressions
-Factor it
-Cancel factors found in the numerator and the denominator
-Multiply / Simplify
Reduce the following fraction

Reduce the following expression

*When we Reduce and simplify algebraic fractions follow the following 5 steps:
1) Factor the numerator and the denominator
2) State the restrictions.
*What would make the denominator have a value of zero?
3) Reduce by any common terms
4) Factor out -1 if necessary
* (a - b) = -1(b - a)
5) Simplify
Eg)
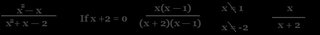
Eg)
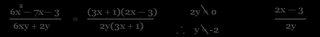
-Factor it
-Cancel factors found in the numerator and the denominator
-Multiply / Simplify
Reduce the following fraction

Reduce the following expression

*When we Reduce and simplify algebraic fractions follow the following 5 steps:
1) Factor the numerator and the denominator
2) State the restrictions.
*What would make the denominator have a value of zero?
3) Reduce by any common terms
4) Factor out -1 if necessary
* (a - b) = -1(b - a)
5) Simplify
Eg)
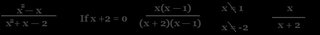
Eg)
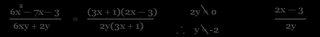
Sorry for being SO late in blogging, Its just that I wasnt feeling very good all weekend. To make up for me being late I will do December 12/06 also
Sorry Couldn't find a link forNon Permissible Values
Do exercises:
42 omit 12
43 omit 11
Thursday, December 07, 2006
posted by Ms. Armstrong at 12:27 p.m.
Here is an interactive site that explains, shows examples, and provides practise with algebraic expressions.
Give it a go!!
Ms. Armstrong
Give it a go!!
Ms. Armstrong
Monday, December 04, 2006
posted by Ms. Armstrong at 9:08 p.m.
Hey Gummy Bears,
Here is a parallelogram problem for you to work on together. You can post comments, solutions, questions, ideas all in the interest of progressing the solution to the problem. Don't forget to use mathematical vocabulary so that everyone will know exactly what you are referring to. (No saying things like the number beside the thingy with the little side. ;^)
If a parallelogram is a non-rigid figure, find the minimum and maximum values for each of the diagonals if the lengths of the sides are 5 and 12.
For anyone wanting extra study tools, don't forget to try the multiple choice quizzes that I posted earlier this month.
Here is a parallelogram problem for you to work on together. You can post comments, solutions, questions, ideas all in the interest of progressing the solution to the problem. Don't forget to use mathematical vocabulary so that everyone will know exactly what you are referring to. (No saying things like the number beside the thingy with the little side. ;^)
If a parallelogram is a non-rigid figure, find the minimum and maximum values for each of the diagonals if the lengths of the sides are 5 and 12.
For anyone wanting extra study tools, don't forget to try the multiple choice quizzes that I posted earlier this month.
Wednesday, November 29, 2006
posted by --thamie-- at 5:57 p.m.
Hiya!!! We didn't do much today in class. We just had a quiz on trigonometry (including sine and cosine laws) and went to the computer lab to find the definitions of the following words:
- complementary angles
- supplementary angles
- consecutive
- polygon
- quadrilateral
- congruent
- diagonal
- bisect
I guess we're doing this to have a heads-up on the geometry section of this unit.
For HOMEWORK ... fill up your Three Point Approach for Words and Concept sheets if you didn't get to finish it in class today.
If you're having any trouble with the definitions, you can go to this >>website<<. (I know the site says "for kids" but I think the activities are pretty cool and helpful.)
Next blogger is Christine !!!
- complementary angles
- supplementary angles
- consecutive
- polygon
- quadrilateral
- congruent
- diagonal
- bisect
I guess we're doing this to have a heads-up on the geometry section of this unit.
For HOMEWORK ... fill up your Three Point Approach for Words and Concept sheets if you didn't get to finish it in class today.
If you're having any trouble with the definitions, you can go to this >>website<<. (I know the site says "for kids" but I think the activities are pretty cool and helpful.)
Next blogger is Christine !!!
Monday, November 27, 2006
posted by Ms. Armstrong at 8:54 p.m.
Hey there Gummy Bears...
Here are some multiple choice quizzes to help you review.
Law of Sines
Law of Cosines
Right angle Triangles
A Challenge
I also came across an interesting question to challenge your brains and stimulate your competitive nature. I would like you to 'discuss' the solution to this question through the comment box. If each person adds their ideas, I would bet that you can get it.
Solve the equation for A and B.
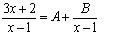
Good luck, have fun, and happy solving :)
Here are some multiple choice quizzes to help you review.
Law of Sines
Law of Cosines
Right angle Triangles
A Challenge
I also came across an interesting question to challenge your brains and stimulate your competitive nature. I would like you to 'discuss' the solution to this question through the comment box. If each person adds their ideas, I would bet that you can get it.
Solve the equation for A and B.
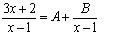
Good luck, have fun, and happy solving :)