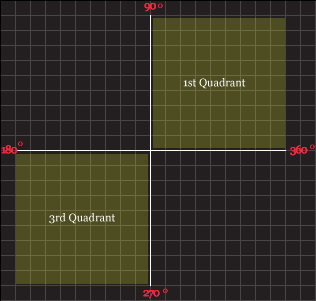
- complementary angles
- supplementary angles
- consecutive
- polygon
- quadrilateral
- congruent
- diagonal
- bisect
I guess we're doing this to have a heads-up on the geometry section of this unit.
For HOMEWORK ... fill up your Three Point Approach for Words and Concept sheets if you didn't get to finish it in class today.
If you're having any trouble with the definitions, you can go to this >>website<<. (I know the site says "for kids" but I think the activities are pretty cool and helpful.)
Next blogger is Christine !!!
Here are some multiple choice quizzes to help you review.
Law of Sines
Law of Cosines
Right angle Triangles
A Challenge
I also came across an interesting question to challenge your brains and stimulate your competitive nature. I would like you to 'discuss' the solution to this question through the comment box. If each person adds their ideas, I would bet that you can get it.
Solve the equation for A and B.
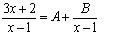
Good luck, have fun, and happy solving :)
Ms. Armstrong gave us a yellow sheet of paper with 2 questions on it. The first question didn't make sense at all so even Ms. Armstrong had some confusion. So we'll omit that so we can focus on the more important stuff.
a) sin(x) = .707 acute angle = ___ obtuse angle = ___
b) cos(x) = .940 acute angle = ___ obtuse angle = ___
c) tan(x) = 11.43 acute angle = ___ obtuse angle = ___
d) cos(x) = -.970 acute angle = ___ obtuse angle = ___
e) sin(x) = -.5 acute angle = ___ obtuse angle = ___
f) tan(x) = -1.43 acute angle = ___ obtuse angle = ___
Note: It's not as easy at it looks. Here's how you solve each of the above questions but first, keep in mind to round all of your degrees to a whole number.
1) To find the acute angle, punch in the equation in your calculator:
2nd function > SIN/COS/TAN button = SIN/COS/TAN-1 (given ratio).
Let's use letter a) for an example.
So, 2nd funct. > SIN button = SIN-1 (.707) : the answer is 45o.
The degree that comes out of this equation is your acute angle.
2) Now let's find the obtuse angle. To find the obtuse angle, you will need to know which quadrant does the given ratio belongs to.
And now you're done your positive ratios! Here's how I solved the first three questions:
2) Then let's find the obtuse angle. Do the same thing as you did to the positive ratios.
d) cos(x) = -.970 which is 166 degrees
acute angle = 166 degrees
obtuse angle = 194 degrees
e) sin(x) = -.5 which is 30 degrees
acute angle = 30 degrees
obtuse angle = 330 degrees
f) tan(x) = -1.43 which is 55 degrees
acute angle = 55 degrees
obtuse angle = 235 degrees
And that's it! Sorry for the delay guys, there was too much in my head, although it's done now (: we also got our unit tests back then we went over some of the questions. Congratulations to the all stars! And oh yeah, I pick Desitini to blog next since the people I know didn't want to since they're "busy", haha. Oh yeah, and reminder to redo question #2 on exercise 18 using the above steps.
Ms. Armstrong, a video for this one is kind of hard to find. If anyone can help me , that'll be great :)
Sm
 all triangle
all triangleNote:
Mrs. Armstrong told us that when using a2 + b 2 = c2 we should use Leg2 + Leg2 = Hyp2 instead, unless it is labeled that way
Medium triangle

Since these are 30* triangles (using Sin) it will have a pattern in the measurements; in other words the hyp will be twice as big as the opp
Large triangle

The adj is effect by the opp of the triangle as you can see through these examples
Relations

Sin : Related to the Y axis
Cos : Related to the X axis
Tan : related to the Y axis divided by the X axis

Here is a chart that will show the relation of the trig ratios
Homework: exercise 18 and the next one to blog is..... Edward
Here is the code that Chris used to create square root symbols. If you need to incorporate it into your post, my suggestion would be to do a copy and paste. The only thing that you will need to do is remove the *'s that I have added in.
x<*big>√<*/big><*span style="BORDER-TOP: white 1px solid">y<*/span>, x=Any number before the root sign and y=What is under the root sign.
I am also putting in some links for reviewing material.
roots and radicals (videos)
rational exponents (tutorial with practice questions)
simplifying radical expressions (m/c quiz)
operations with radicals (m/c quiz)
Hope this helps and have fun!!!
Ms Armstrong
You can only add and subtract like terms.
2√2 + 3√2 = 5√2
These two examples can be added together because
their bases are the same.
5x+3y=5x+3y
4√2 + 3√3 = 4√2 + 3√3
In order to add/subtract radicals you must first simplify.
2√4·3 - 3√16·3 (Break the problem up so there's a perfect square under the root)
4√3 - 12√3 (Solve the perfect square and multiply it with the number at the front, if there's no number in front, its considered to be a 1)
-8√3 (Combine like terms)
√4·3 - 2√4·2 - 3√25·3 + √2 (Break the problem up with the highest perfect square that can be multiplyed into the original number)
2√3 - 4√2 - 15√3 + √2 (Solve the perfect square and multiply it with the number at the front, if there's no number in front, its considered to be a 1)
-13√3 + 5√2 (Combine like terms)
Note: The next example has the cube root represented by an upper 3.
Example: 3√24 + 3√81 + 2√12 - 3√48 (Starting problem)
3√8·3 + 3√27·3 + 2√4·3 - 3√16·3 (Break up the problem with the highest perfect cube that can be multiplyed into the original number)
23√3 + 33√3 + 4√3 - 12√3 (Solve the perfect cube and multiply it with the number at the front, if there's no number in front, it's considered to be a 1)
5·3√3 - 8√3(Combine like terms, remember to keep square, cube etc. roots seperated.)
Example: 6x√x - 7√x3 (Starting problem)
6x√x - 7x√x (Since this problem is rather easy, we can just look at it and take out x2 from x3 which leaves us with x)
-x√x (Combine like terms)
Homework was Exercise #34 omitting 10,16,18. If there's any questions feel free to comment. If you need any additional help, click here to view a page about radicals.
Originally posted by Jamie:
"The next person who will post will be "tall guy" Chris. Yes you. Haha. Mwahahahhaha.... =D"The next person who will post will be the "small person" Jamie. Yes you. Haha. Mwahahahhaha....=D